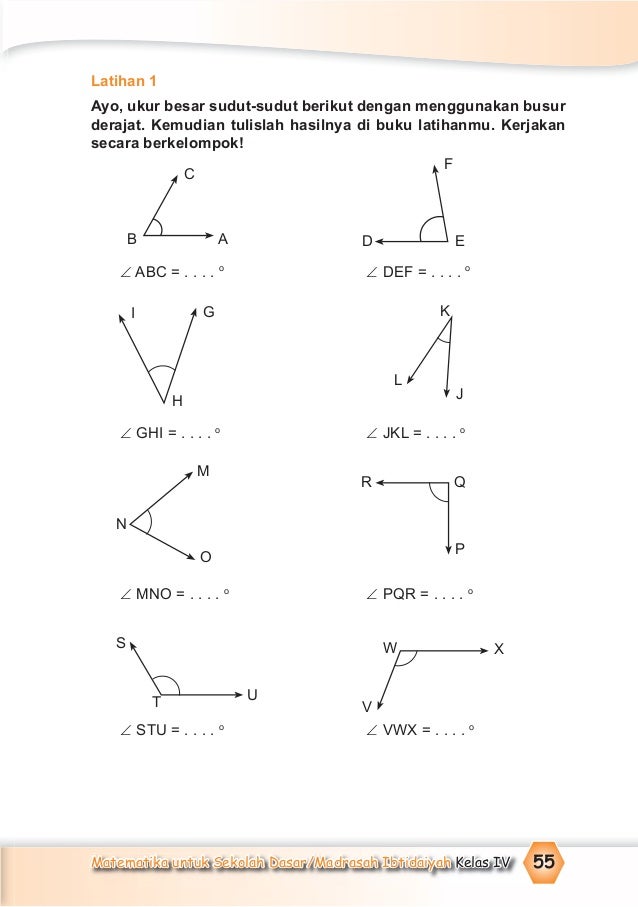
Mengenal dan memahami bangun datar merupakan salah satu pondasi penting dalam pembelajaran matematika di jenjang sekolah dasar. Pada kelas 4 semester 1, siswa akan diperkenalkan pada berbagai jenis bangun datar, sifat-sifatnya, serta cara menghitung luas dan kelilingnya. Kemampuan ini tidak hanya penting untuk mata pelajaran matematika itu sendiri, tetapi juga memiliki aplikasi luas dalam kehidupan sehari-hari. Agar pemahaman siswa semakin kokoh dan mendalam, latihan soal yang terstruktur dan bervariasi menjadi kunci utama.
Artikel ini akan membahas secara mendalam mengenai latihan soal matematika kelas 4 semester 1 yang fokus pada materi bangun datar. Kita akan mengupas tuntas jenis-jenis bangun datar yang umum dipelajari, konsep-konsep kunci yang perlu dikuasai, serta menyajikan berbagai contoh soal yang dapat membantu siswa berlatih dan mengasah kemampuannya.
Memahami Konsep Dasar Bangun Datar
Sebelum terjun ke latihan soal, penting untuk mereview kembali konsep-konsep dasar mengenai bangun datar. Bangun datar adalah bangun dua dimensi yang dibatasi oleh garis-garis lurus atau lengkung. Beberapa bangun datar yang umum dipelajari di kelas 4 semester 1 antara lain:
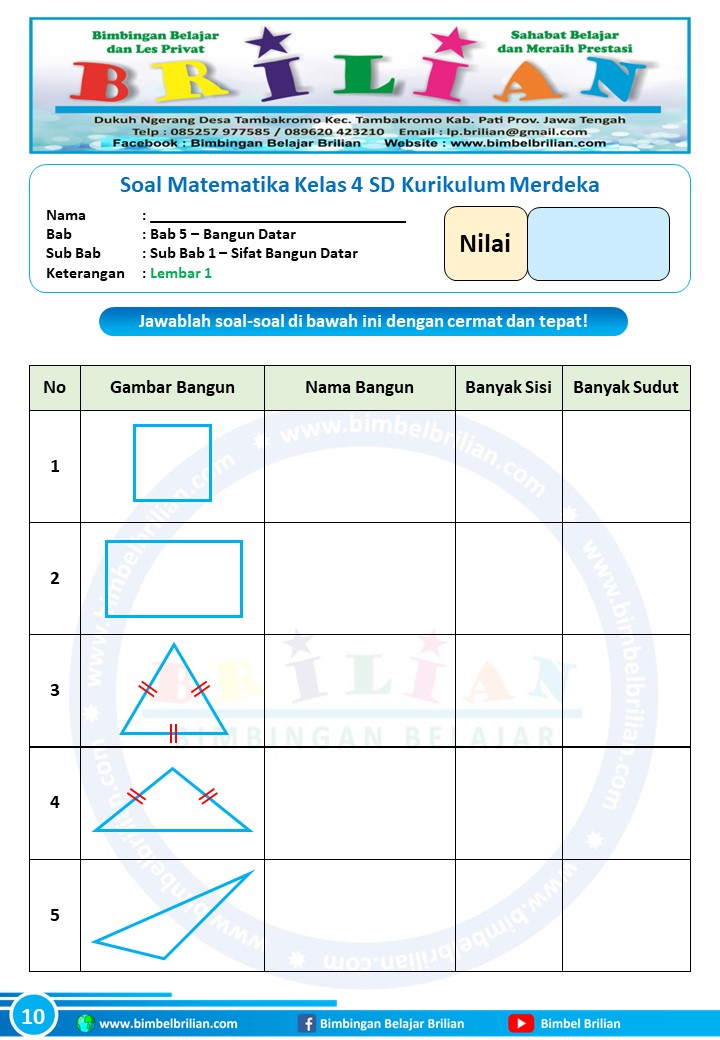
- Persegi: Bangun datar yang memiliki empat sisi sama panjang dan empat sudut siku-siku (90 derajat).
- Persegi Panjang: Bangun datar yang memiliki dua pasang sisi berhadapan sama panjang dan sejajar, serta empat sudut siku-siku.
- Segitiga: Bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga memiliki berbagai jenis berdasarkan panjang sisinya (segitiga sama sisi, sama kaki, sembarang) dan besar sudutnya (segitiga siku-siku, lancip, tumpul).
- Lingkaran: Bangun datar yang merupakan himpunan semua titik pada bidang datar yang berjarak sama dari suatu titik pusat.
- Jajar Genjang: Bangun datar yang memiliki dua pasang sisi berhadapan sama panjang dan sejajar. Sudut-sudut yang berhadapan sama besar.
- Belah Ketupat: Bangun datar yang memiliki empat sisi sama panjang. Sudut-sudut yang berhadapan sama besar dan diagonal-diagonalnya saling tegak lurus serta membagi dua sama panjang.
- Trapesium: Bangun datar yang memiliki sepasang sisi sejajar. Trapesium juga memiliki beberapa jenis (siku-siku, sama kaki, sembarang).
Selain mengenal jenis-jenis bangun datar, siswa juga perlu memahami konsep keliling dan luas.
- Keliling adalah panjang total garis yang membentuk batas luar bangun datar.
- Luas adalah ukuran area atau besarnya daerah yang ditempati oleh bangun datar tersebut.
Rumus-Rumus Penting yang Perlu Dikuasai
Dalam latihan soal, siswa akan sering dihadapkan pada penggunaan rumus untuk menghitung keliling dan luas. Berikut adalah rumus-rumus dasar yang perlu diingat:
- Persegi:
- Keliling = 4 x sisi (K = 4s)
- Luas = sisi x sisi (L = s²)
- Persegi Panjang:
- Keliling = 2 x (panjang + lebar) (K = 2(p + l))
- Luas = panjang x lebar (L = p x l)
- Segitiga:
- Keliling = sisi1 + sisi2 + sisi3 (K = a + b + c)
- Luas = ½ x alas x tinggi (L = ½ x a x t)
- Lingkaran:
- Keliling = 2 x π x jari-jari (K = 2πr) atau Keliling = π x diameter (K = πd)
- Luas = π x jari-jari x jari-jari (L = πr²)
(Nilai π biasanya dibulatkan menjadi 22/7 atau 3.14)
- Jajar Genjang:
- Keliling = 2 x (sisi1 + sisi2) (K = 2(a + b))
- Luas = alas x tinggi (L = a x t)
- Belah Ketupat:
- Keliling = 4 x sisi (K = 4s)
- Luas = ½ x diagonal1 x diagonal2 (L = ½ x d1 x d2)
- Trapesium:
- Keliling = sisi1 + sisi2 + sisi3 + sisi4 (K = a + b + c + d)
- Luas = ½ x (jumlah sisi sejajar) x tinggi (L = ½ x (a + b) x t)
Strategi Efektif dalam Mengerjakan Latihan Soal
Untuk memaksimalkan hasil dari latihan soal, siswa perlu menerapkan beberapa strategi:
- Pahami Pertanyaan: Baca soal dengan cermat dan identifikasi informasi penting yang diberikan, termasuk jenis bangun datar, ukuran yang diketahui (panjang sisi, lebar, jari-jari, alas, tinggi, diagonal), dan apa yang ditanyakan (keliling atau luas).
- Gambar Ilustrasi: Jika soal tidak menyertakan gambar, buatlah sketsa sederhana dari bangun datar yang dimaksud. Ini akan membantu memvisualisasikan masalah dan mengidentifikasi elemen-elemen yang relevan.
- Identifikasi Rumus yang Tepat: Berdasarkan jenis bangun datar dan apa yang ditanyakan, pilih rumus keliling atau luas yang sesuai.
- Substitusikan Nilai: Masukkan nilai-nilai yang diketahui ke dalam rumus yang dipilih.
- Hitung dengan Teliti: Lakukan perhitungan matematika dengan hati-hati, perhatikan urutan operasi jika diperlukan.
- Sertakan Satuan: Jangan lupa untuk menyertakan satuan yang tepat pada jawaban akhir (misalnya, cm, m, cm², m²).
- Periksa Kembali: Setelah selesai menghitung, periksa kembali langkah-langkah dan perhitungan Anda untuk memastikan tidak ada kesalahan.
Contoh Latihan Soal dan Pembahasan
Mari kita berlatih dengan beberapa contoh soal yang bervariasi:
Soal 1 (Persegi):
Sebuah taman berbentuk persegi memiliki panjang sisi 15 meter. Berapakah keliling dan luas taman tersebut?
Pembahasan:
-
Jenis bangun datar: Persegi
-
Diketahui: sisi (s) = 15 meter
-
Ditanya: Keliling (K) dan Luas (L)
-
Rumus Keliling Persegi: K = 4s
K = 4 x 15 meter
K = 60 meter -
Rumus Luas Persegi: L = s²
L = 15 meter x 15 meter
L = 225 meter persegi
Jadi, keliling taman adalah 60 meter dan luasnya adalah 225 meter persegi.
Soal 2 (Persegi Panjang):
Sebuah meja belajar berbentuk persegi panjang memiliki panjang 120 cm dan lebar 80 cm. Hitunglah keliling dan luas permukaan meja belajar tersebut.
Pembahasan:
-
Jenis bangun datar: Persegi Panjang
-
Diketahui: panjang (p) = 120 cm, lebar (l) = 80 cm
-
Ditanya: Keliling (K) dan Luas (L)
-
Rumus Keliling Persegi Panjang: K = 2(p + l)
K = 2(120 cm + 80 cm)
K = 2(200 cm)
K = 400 cm -
Rumus Luas Persegi Panjang: L = p x l
L = 120 cm x 80 cm
L = 9600 cm persegi
Jadi, keliling meja belajar adalah 400 cm dan luas permukaannya adalah 9600 cm persegi.
Soal 3 (Segitiga):
Sebuah segitiga memiliki alas 20 cm dan tinggi 12 cm. Hitunglah luas segitiga tersebut.
Pembahasan:
-
Jenis bangun datar: Segitiga
-
Diketahui: alas (a) = 20 cm, tinggi (t) = 12 cm
-
Ditanya: Luas (L)
-
Rumus Luas Segitiga: L = ½ x a x t
L = ½ x 20 cm x 12 cm
L = 10 cm x 12 cm
L = 120 cm persegi
Jadi, luas segitiga tersebut adalah 120 cm persegi.
Soal 4 (Lingkaran):
Sebuah roda sepeda memiliki jari-jari 35 cm. Jika π = 22/7, hitunglah keliling roda sepeda tersebut.
Pembahasan:
-
Jenis bangun datar: Lingkaran
-
Diketahui: jari-jari (r) = 35 cm, π = 22/7
-
Ditanya: Keliling (K)
-
Rumus Keliling Lingkaran: K = 2πr
K = 2 x (22/7) x 35 cm
K = 2 x 22 x (35/7) cm
K = 2 x 22 x 5 cm
K = 44 x 5 cm
K = 220 cm
Jadi, keliling roda sepeda tersebut adalah 220 cm.
Soal 5 (Jajar Genjang):
Sebuah kain berbentuk jajar genjang memiliki panjang alas 50 cm dan tinggi 30 cm. Berapakah luas kain tersebut?
Pembahasan:
-
Jenis bangun datar: Jajar Genjang
-
Diketahui: alas (a) = 50 cm, tinggi (t) = 30 cm
-
Ditanya: Luas (L)
-
Rumus Luas Jajar Genjang: L = a x t
L = 50 cm x 30 cm
L = 1500 cm persegi
Jadi, luas kain tersebut adalah 1500 cm persegi.
Soal 6 (Belah Ketupat):
Dua diagonal sebuah belah ketupat memiliki panjang 18 cm dan 24 cm. Hitunglah luas belah ketupat tersebut.
Pembahasan:
-
Jenis bangun datar: Belah Ketupat
-
Diketahui: diagonal1 (d1) = 18 cm, diagonal2 (d2) = 24 cm
-
Ditanya: Luas (L)
-
Rumus Luas Belah Ketupat: L = ½ x d1 x d2
L = ½ x 18 cm x 24 cm
L = 9 cm x 24 cm
L = 216 cm persegi
Jadi, luas belah ketupat tersebut adalah 216 cm persegi.
Soal 7 (Trapesium):
Sebuah taman berbentuk trapesium memiliki panjang sisi sejajar 10 meter dan 16 meter. Tinggi taman tersebut adalah 8 meter. Berapakah luas taman tersebut?
Pembahasan:
-
Jenis bangun datar: Trapesium
-
Diketahui: sisi sejajar (a) = 10 meter, sisi sejajar (b) = 16 meter, tinggi (t) = 8 meter
-
Ditanya: Luas (L)
-
Rumus Luas Trapesium: L = ½ x (a + b) x t
L = ½ x (10 meter + 16 meter) x 8 meter
L = ½ x (26 meter) x 8 meter
L = 13 meter x 8 meter
L = 104 meter persegi
Jadi, luas taman tersebut adalah 104 meter persegi.
Latihan Tambahan dan Tingkat Kesulitan
Selain contoh-contoh di atas, siswa dapat dilatih dengan variasi soal yang lebih menantang, seperti:
- Soal Cerita yang Lebih Kompleks: Soal yang menggabungkan beberapa bangun datar atau membutuhkan beberapa langkah perhitungan untuk menemukan jawaban.
- Menemukan Ukuran yang Hilang: Diberikan luas atau keliling, siswa diminta mencari panjang sisi, lebar, jari-jari, atau tinggi.
- Perbandingan Luas atau Keliling: Membandingkan luas atau keliling dari dua bangun datar yang berbeda.
- Soal Pilihan Ganda dan Isian Singkat: Variasi format soal untuk menguji pemahaman secara menyeluruh.
Manfaat Latihan Soal yang Konsisten
Melakukan latihan soal secara konsisten memberikan banyak manfaat bagi siswa kelas 4 semester 1, antara lain:
- Memperkuat Pemahaman Konsep: Latihan membantu menginternalisasi rumus dan konsep bangun datar.
- Meningkatkan Keterampilan Berhitung: Siswa menjadi lebih terampil dalam melakukan operasi matematika.
- Membangun Kepercayaan Diri: Semakin banyak berlatih, siswa akan semakin percaya diri dalam menghadapi soal-soal matematika.
- Mengidentifikasi Area yang Perlu Perbaikan: Dengan menganalisis kesalahan, siswa dapat mengetahui bagian mana yang masih perlu dipelajari lebih lanjut.
- Mempersiapkan Diri untuk Ujian: Latihan soal adalah cara terbaik untuk mempersiapkan diri menghadapi penilaian harian, tengah semester, maupun akhir semester.
Kesimpulan
Mempelajari bangun datar merupakan bagian integral dari kurikulum matematika kelas 4 semester 1. Dengan pemahaman konsep yang kuat dan latihan soal yang terstruktur, siswa dapat menguasai materi ini dengan baik. Guru dan orang tua memiliki peran penting dalam menyediakan sumber latihan yang beragam dan memotivasi siswa untuk terus berlatih. Ingatlah, konsistensi adalah kunci. Melalui latihan yang tekun, siswa tidak hanya akan mahir dalam menghitung keliling dan luas bangun datar, tetapi juga akan membangun fondasi matematika yang kuat untuk masa depan mereka. Selamat berlatih!