Matematika, khususnya pada jenjang kelas 4 Sekolah Dasar, seringkali menjadi gerbang awal bagi anak-anak untuk memahami dunia di sekitar mereka melalui konsep-konsep abstrak. Salah satu topik fundamental yang diajarkan adalah bangun datar. Bangun datar, seperti persegi, persegi panjang, segitiga, lingkaran, dan trapesium, adalah bentuk-bentuk dua dimensi yang membentuk banyak objek dalam kehidupan sehari-hari. Memahami sifat-sifat dan cara menghitung luas serta keliling bangun datar bukan hanya keterampilan akademis, tetapi juga bekal penting untuk pemecahan masalah praktis.
Artikel ini akan membahas secara mendalam tentang latihan soal matematika kelas 4 yang berfokus pada bangun datar. Kita akan menelusuri pentingnya latihan soal, jenis-jenis bangun datar yang umum dipelajari, serta menyajikan berbagai contoh soal yang dirancang untuk memperkuat pemahaman siswa, mulai dari konsep dasar hingga tingkat yang lebih menantang.
Mengapa Latihan Soal Bangun Datar Begitu Penting?
Latihan soal bukanlah sekadar rutinitas untuk memenuhi kurikulum. Bagi siswa kelas 4, latihan soal bangun datar memiliki peran krusial dalam:
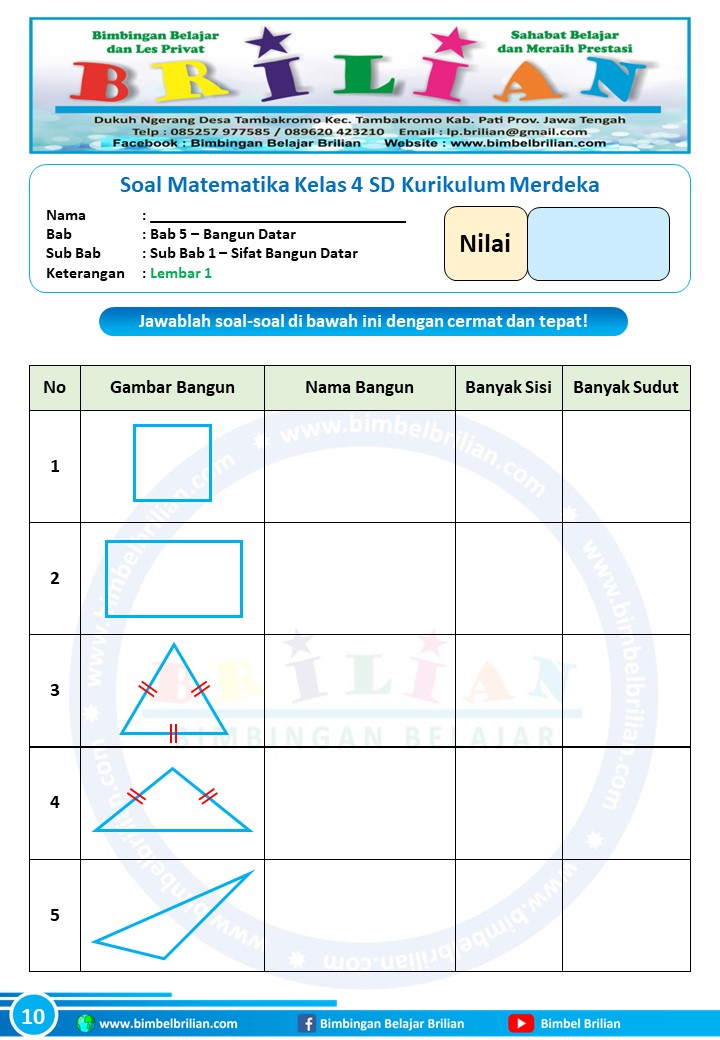
- Memperkuat Konsep Dasar: Pengulangan melalui soal-soal latihan membantu siswa menginternalisasi definisi, sifat-sifat, dan rumus-rumus yang berkaitan dengan setiap bangun datar.
- Mengembangkan Keterampilan Pemecahan Masalah: Soal-soal yang bervariasi melatih siswa untuk menganalisis masalah, mengidentifikasi informasi yang relevan, memilih strategi yang tepat, dan menerapkan rumus dengan benar.
- Meningkatkan Kepercayaan Diri: Ketika siswa berhasil menyelesaikan soal-soal latihan, mereka akan merasa lebih percaya diri dalam kemampuan matematika mereka. Keberhasilan kecil ini akan memotivasi mereka untuk terus belajar.
- Mengidentifikasi Area yang Perlu Perbaikan: Latihan soal membantu guru dan orang tua mengetahui bagian mana dari materi bangun datar yang masih sulit dipahami oleh siswa, sehingga intervensi yang tepat dapat diberikan.
- Menghubungkan Matematika dengan Kehidupan Nyata: Banyak soal dibangun datar dirancang dengan konteks dunia nyata, seperti menghitung luas taman, menghitung panjang pagar, atau menghitung keliling meja. Ini menunjukkan relevansi matematika dalam kehidupan sehari-hari.
Mengenal Bangun Datar Umum di Kelas 4
Sebelum masuk ke latihan soal, mari kita ingatkan kembali tentang bangun datar yang paling sering ditemui di kelas 4:
- Persegi: Bangun datar dengan empat sisi sama panjang dan empat sudut siku-siku (90 derajat).
- Rumus Luas: sisi × sisi (s²)
- Rumus Keliling: 4 × sisi (4s)
- Persegi Panjang: Bangun datar dengan empat sisi, di mana sisi-sisi yang berhadapan sama panjang dan sejajar, serta empat sudut siku-siku.
- Rumus Luas: panjang × lebar (p × l)
- Rumus Keliling: 2 × (panjang + lebar) (2(p + l))
- Segitiga: Bangun datar dengan tiga sisi dan tiga sudut. Ada berbagai jenis segitiga (sama sisi, sama kaki, siku-siku, sembarang), namun rumus luas umumnya sama.
- Rumus Luas: ½ × alas × tinggi
- Rumus Keliling: jumlah panjang ketiga sisinya
- Lingkaran: Bangun datar yang terdiri dari semua titik pada bidang yang berjarak sama dari satu titik pusat.
- Rumus Luas: π × jari-jari × jari-jari (πr²) (Biasanya menggunakan π ≈ 22/7 atau 3.14)
- Rumus Keliling (Lingkar): 2 × π × jari-jari (2πr) atau π × diameter (πd)
- Trapesium: Bangun datar dengan empat sisi, di mana terdapat sepasang sisi sejajar.
- Rumus Luas: ½ × (jumlah sisi sejajar) × tinggi
- Rumus Keliling: jumlah panjang keempat sisinya
Latihan Soal Matematika Kelas 4 Bangun Datar: Beragam Tingkatan
Mari kita mulai dengan contoh-contoh soal yang dikategorikan berdasarkan tingkat kesulitannya.
Tingkat 1: Konsep Dasar dan Penerapan Rumus Langsung
Pada tingkat ini, siswa diminta untuk menerapkan rumus secara langsung setelah mengidentifikasi bangun datar dan informasi yang diberikan.
-
Soal Persegi:
Sebuah taman berbentuk persegi memiliki panjang sisi 7 meter. Berapakah luas taman tersebut?- Pembahasan: Kita tahu bahwa luas persegi adalah sisi × sisi. Sisi taman adalah 7 meter. Maka, luas taman = 7 m × 7 m = 49 meter persegi.
-
Soal Persegi Panjang:
Sebuah buku memiliki panjang 25 cm dan lebar 18 cm. Hitunglah keliling buku tersebut.- Pembahasan: Keliling persegi panjang adalah 2 × (panjang + lebar). Panjang = 25 cm, lebar = 18 cm. Keliling = 2 × (25 cm + 18 cm) = 2 × 43 cm = 86 cm.
-
Soal Segitiga:
Sebuah segitiga memiliki alas 10 cm dan tinggi 6 cm. Berapakah luas segitiga tersebut?- Pembahasan: Luas segitiga = ½ × alas × tinggi. Alas = 10 cm, tinggi = 6 cm. Luas = ½ × 10 cm × 6 cm = ½ × 60 cm² = 30 cm persegi.
-
Soal Lingkaran (dengan jari-jari diketahui):
Jari-jari sebuah roda sepeda adalah 21 cm. Hitunglah keliling roda tersebut. (Gunakan π = 22/7)- Pembahasan: Keliling lingkaran = 2 × π × jari-jari. Jari-jari = 21 cm. Keliling = 2 × (22/7) × 21 cm = 2 × 22 × 3 cm = 132 cm.
-
Soal Trapesium:
Sebuah trapesium memiliki panjang sisi sejajar 8 cm dan 12 cm. Jika tingginya 5 cm, berapakah luas trapesium tersebut?- Pembahasan: Luas trapesium = ½ × (jumlah sisi sejajar) × tinggi. Sisi sejajar = 8 cm dan 12 cm. Tinggi = 5 cm. Luas = ½ × (8 cm + 12 cm) × 5 cm = ½ × 20 cm × 5 cm = ½ × 100 cm² = 50 cm persegi.
Tingkat 2: Menemukan Salah Satu Dimensi yang Hilang
Pada tingkat ini, siswa diberikan luas atau keliling, dan diminta untuk mencari panjang salah satu sisinya.
-
Soal Persegi:
Luas sebuah persegi adalah 81 cm persegi. Berapakah panjang sisi persegi tersebut?- Pembahasan: Luas persegi = sisi × sisi. Kita mencari angka yang jika dikalikan dengan dirinya sendiri hasilnya 81. Angka tersebut adalah 9. Jadi, panjang sisinya adalah 9 cm.
-
Soal Persegi Panjang:
Sebuah lapangan berbentuk persegi panjang memiliki luas 120 meter persegi. Jika panjang lapangan tersebut adalah 15 meter, berapakah lebarnya?- Pembahasan: Luas persegi panjang = panjang × lebar. Kita tahu luas (120 m²) dan panjang (15 m). Maka, lebar = Luas / panjang = 120 m² / 15 m = 8 meter.
-
Soal Segitiga:
Luas sebuah segitiga adalah 45 cm persegi. Jika alas segitiga tersebut adalah 15 cm, berapakah tingginya?- Pembahasan: Luas segitiga = ½ × alas × tinggi. Kita punya luas (45 cm²) dan alas (15 cm). Maka, 45 cm² = ½ × 15 cm × tinggi. Agar lebih mudah, kita bisa kalikan kedua sisi dengan 2: 90 cm² = 15 cm × tinggi. Tinggi = 90 cm² / 15 cm = 6 cm.
-
Soal Lingkaran (dengan keliling diketahui):
Keliling sebuah lingkaran adalah 88 cm. Berapakah jari-jari lingkaran tersebut? (Gunakan π = 22/7)- Pembahasan: Keliling lingkaran = 2 × π × jari-jari. Kita punya keliling (88 cm) dan π. Maka, 88 cm = 2 × (22/7) × jari-jari. 88 cm = (44/7) × jari-jari. Jari-jari = 88 cm × (7/44) = 2 × 7 cm = 14 cm.
Tingkat 3: Soal Kombinasi dan Pemecahan Masalah yang Lebih Kompleks
Tingkat ini melibatkan gabungan bangun datar, soal cerita yang memerlukan analisis lebih mendalam, atau penerapan konsep keliling dan luas dalam satu masalah.
-
Soal Kombinasi (Persegi dan Persegi Panjang):
Sebuah gambar memiliki dua bagian. Bagian pertama adalah persegi dengan sisi 10 cm. Bagian kedua adalah persegi panjang yang menempel pada salah satu sisi persegi tersebut, dengan panjang 15 cm dan lebar sama dengan sisi persegi. Berapakah total luas gambar tersebut?- Pembahasan:
- Luas persegi = sisi × sisi = 10 cm × 10 cm = 100 cm persegi.
- Lebar persegi panjang = sisi persegi = 10 cm. Panjang persegi panjang = 15 cm.
- Luas persegi panjang = panjang × lebar = 15 cm × 10 cm = 150 cm persegi.
- Total luas = Luas persegi + Luas persegi panjang = 100 cm² + 150 cm² = 250 cm persegi.
- Pembahasan:
-
Soal Cerita (Keliling):
Ayah ingin memasang pagar di sekeliling kebunnya yang berbentuk persegi panjang. Panjang kebun adalah 20 meter dan lebarnya 12 meter. Jika harga 1 meter pagar adalah Rp 50.000, berapakah total biaya yang dibutuhkan Ayah untuk memasang pagar?- Pembahasan:
- Pertama, kita hitung keliling kebun. Keliling = 2 × (panjang + lebar) = 2 × (20 m + 12 m) = 2 × 32 m = 64 meter.
- Selanjutnya, kita hitung total biaya. Total biaya = keliling × harga per meter = 64 m × Rp 50.000/m = Rp 3.200.000.
- Pembahasan:
-
Soal Cerita (Luas):
Sebuah dinding kamar berukuran panjang 4 meter dan tinggi 3 meter. Dinding tersebut akan dicat ulang. Namun, ada jendela berukuran 2 meter × 1.5 meter yang tidak akan dicat. Berapakah luas dinding yang akan dicat?- Pembahasan:
- Luas dinding seluruhnya = panjang × tinggi = 4 m × 3 m = 12 meter persegi.
- Luas jendela = panjang × lebar = 2 m × 1.5 m = 3 meter persegi.
- Luas dinding yang dicat = Luas dinding seluruhnya – Luas jendela = 12 m² – 3 m² = 9 meter persegi.
- Pembahasan:
-
Soal Menggunakan Perbandingan (Opsional untuk kelas 4 yang lebih mahir):
Panjang sebuah persegi panjang adalah dua kali lebarnya. Jika keliling persegi panjang tersebut adalah 30 cm, berapakah luasnya?- Pembahasan:
- Misalkan lebar = l, maka panjang = 2l.
- Keliling = 2 × (panjang + lebar)
- 30 cm = 2 × (2l + l)
- 30 cm = 2 × (3l)
- 30 cm = 6l
- l = 30 cm / 6 = 5 cm.
- Jadi, lebar = 5 cm dan panjang = 2 × 5 cm = 10 cm.
- Luas = panjang × lebar = 10 cm × 5 cm = 50 cm persegi.
- Pembahasan:
Tips untuk Latihan Soal yang Efektif
- Mulai dari yang Mudah: Jangan langsung menyerah jika menemukan soal yang sulit. Mulailah dengan soal-soal yang lebih sederhana untuk membangun dasar yang kuat.
- Pahami Soal: Baca soal dengan teliti. Identifikasi informasi apa yang diberikan dan apa yang ditanyakan.
- Gambar Bangun Datar: Jika memungkinkan, gambarlah bangun datar yang disebutkan dalam soal. Ini sangat membantu visualisasi.
- Tuliskan Rumus: Selalu tuliskan rumus yang relevan sebelum menghitung. Ini membantu mengurangi kesalahan.
- Periksa Kembali Jawaban: Setelah selesai, periksa kembali perhitungan Anda. Apakah jawabannya masuk akal?
- Diskusi: Jangan ragu untuk bertanya kepada guru atau teman jika ada soal yang tidak dipahami. Diskusi bisa membuka wawasan baru.
- Variasi Soal: Gunakan berbagai sumber latihan soal, baik dari buku teks, lembar kerja, maupun sumber online.
Kesimpulan
Menguasai bangun datar adalah salah satu fondasi penting dalam pembelajaran matematika kelas 4. Melalui latihan soal yang terstruktur dan bervariasi, siswa dapat memperdalam pemahaman mereka, mengembangkan keterampilan pemecahan masalah, dan membangun kepercayaan diri. Ingatlah bahwa proses belajar adalah sebuah perjalanan, dan konsistensi dalam berlatih adalah kunci keberhasilan. Dengan pendekatan yang tepat dan latihan yang menyenangkan, bangun datar akan menjadi topik yang menarik dan mudah dikuasai oleh setiap siswa kelas 4.